|
|
|
An
![]() 3-D version of the Magic Square in which the
3-D version of the Magic Square in which the ![]() rows,
rows, ![]() columns,
columns, ![]() pillars (or
``files''), and four space diagonals each sum to a single number
pillars (or
``files''), and four space diagonals each sum to a single number ![]() known as the Magic Constant. If the
cross-section diagonals also sum to
known as the Magic Constant. If the
cross-section diagonals also sum to ![]() , the magic cube is called a Perfect Magic Cube; if they do not, the cube is
called a Semiperfect Magic Cube, or sometimes an Andrews Cube (Gardner 1988). A pandiagonal cube is a perfect or
semiperfect magic cube which is magic not only along the main space diagonals, but also on the broken space diagonals.
, the magic cube is called a Perfect Magic Cube; if they do not, the cube is
called a Semiperfect Magic Cube, or sometimes an Andrews Cube (Gardner 1988). A pandiagonal cube is a perfect or
semiperfect magic cube which is magic not only along the main space diagonals, but also on the broken space diagonals.
A magic cube using the numbers 1, 2, ..., ![]() , if it exists, has Magic Constant
, if it exists, has Magic Constant
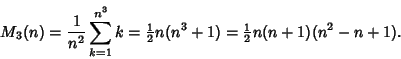
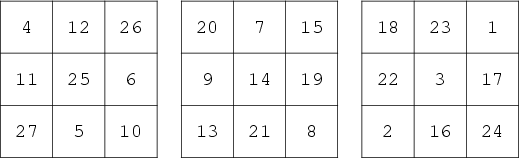
The above semiperfect magic cubes of orders three (Hunter and Madachy 1975, p. 31; Ball and Coxeter 1987, p. 218) and four
(Ball and Coxeter 1987, p. 220) have magic constants 42 and 130, respectively. There is a trivial semiperfect magic cube of
order one, but no semiperfect cubes of orders two or three exist. Semiperfect cubes of Odd order with ![]() and
Doubly Even order can be constructed by extending the methods used for Magic
Squares.
and
Doubly Even order can be constructed by extending the methods used for Magic
Squares.
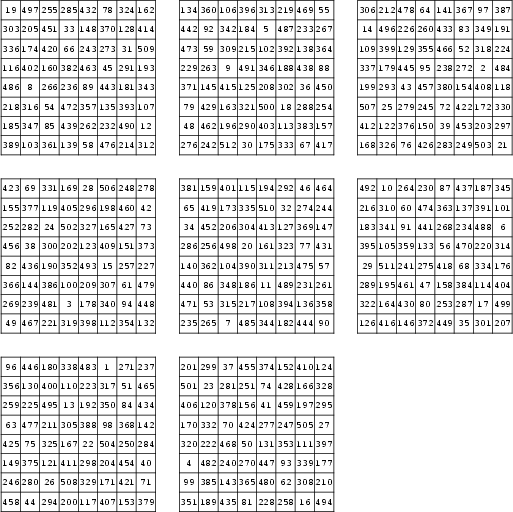
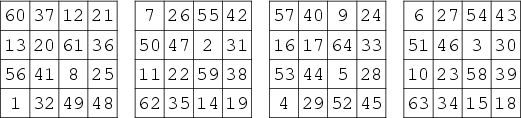
There are no perfect magic cubes of order four (Beeler et al. 1972, Item 50; Gardner 1988). No perfect magic cubes of order five are known, although it is known that such a cube must have a central value of 63 (Beeler et al. 1972, Item 51; Gardner 1988). No order-six perfect magic cubes are known, but Langman (1962) constructed a perfect magic cube of order seven. An order-eight perfect magic cube was published anonymously in 1875 (Barnard 1888, Benson and Jacoby 1981, Gardner 1988). The construction of such a cube is discussed in Ball and Coxeter (1987). Rosser and Walker rediscovered the order-eight cube in the late 1930s (but did not publish it), and Myers independently discovered the cube illustrated above in 1970 (Gardner 1988). Order 9 and 11 magic cubes have also been discovered, but none of order 10 (Gardner 1988).
Semiperfect pandiagonal cubes exist for all orders ![]() and all Odd
and all Odd ![]() (Ball and Coxeter 1987). A perfect pandiagonal
magic cube has been constructed by Planck (1950), cited in Gardner (1988).
(Ball and Coxeter 1987). A perfect pandiagonal
magic cube has been constructed by Planck (1950), cited in Gardner (1988).
Berlekamp et al. (1982, p. 783) give a magic Tesseract.
See also Magic Constant, Magic Graph, Magic Hexagon, Magic Square
References
Adler, A. and Li, S.-Y. R. ``Magic Cubes and Prouhet Sequences.'' Amer. Math. Monthly 84, 618-627, 1977.
Andrews, W. S. Magic Squares and Cubes, 2nd rev. ed. New York: Dover, 1960.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 216-224, 1987.
Barnard, F. A. P. ``Theory of Magic Squares and Cubes.'' Mem. Nat. Acad. Sci. 4, 209-270, 1888.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Benson, W. H. and Jacoby, O. Magic Cubes: New Recreations. New York: Dover, 1981.
Berlekamp, E. R.; Conway, J. H; and Guy, R. K.
Winning Ways, For Your Mathematical Plays, Vol. 2: Games in Particular. London: Academic Press, 1982.
Gardner, M. ``Magic Squares and Cubes.'' Ch. 17 in Time Travel and Other Mathematical Bewilderments.
New York: W. H. Freeman, pp. 213-225, 1988.
Hendricks, J. R. ``Ten Magic Tesseracts of Order Three.'' J. Recr. Math. 18, 125-134, 1985-1986.
Hirayama, A. and Abe, G. Researches in Magic Squares. Osaka, Japan: Osaka Kyoikutosho, 1983.
Hunter, J. A. H. and Madachy, J. S. ``Mystic Arrays.'' Ch. 3 in Mathematical Diversions. New York: Dover, p. 31, 1975.
Langman, H. Play Mathematics. New York: Hafner, pp. 75-76, 1962.
Lei, A. ``Magic Cube and Hypercube.'' http://www.cs.ust.hk/~philipl/magic/mcube2.html.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 99-100, 1979.
Pappas, T. ``A Magic Cube.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 77, 1989.
Planck, C. Theory of Path Nasiks. Rugby, England: Privately Published, 1905.
Rosser, J. B. and Walker, R. J. ``The Algebraic Theory of Diabolical Squares.'' Duke Math. J. 5, 705-728, 1939.
Sloane, N. J. A. Sequence
A027441
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Wynne, B. E. ``Perfect Magic Cubes of Order 7.'' J. Recr. Math. 8, 285-293, 1975-1976.
|
|
|
© 1996-9 Eric W. Weisstein