Magic Constant

The number

$$M_2(n)={1\over n}\sum_{k=1}^{n^2} k = {\textstyle{1\over 2}}n(n^2+1)$$

to which the $n$ numbers in any horizontal, vertical, or main diagonal line must sum in a Magic Square. The first few values are 1, 5 (no such magic square), 15, 34, 65, 111, 175, 260, ... (Sloane's A006003). The magic constant for an $n$th order magic square starting with an Integer $A$ and with entries in an increasing Arithmetic Series with difference $D$ between terms is

$$M_2(n;A,D)={\textstyle{1\over 2}}n[2a+D(n^2-1)]$$

(Hunter and Madachy 1975, Madachy 1979). In a Panmagic Square, in addition to the main diagonals, the broken diagonals also sum to $M_2(n)$.

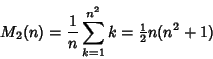
For a Magic Cube, the magic constant is

$$M_3(n)={1\over n^2}\sum_{k=1}^{n^3} k = {\textstyle{1\over 2}}n(n^3+1) = {\textstyle{1\over 2}}n(1+n)(n^2-n+1).$$

The first few values are 1, 9, 42, 130, 315, 651, 1204, ... (Sloane's A027441).

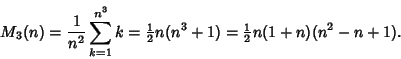
There is a corresponding multiplicative magic constant for Multiplication Magic Squares.

See also Magic Cube, Magic Geometric Constants, Magic Hexagon, Magic Square, Multiplication Magic Square, Panmagic Square

References

Hunter, J. A. H. and Madachy, J. S. ``Mystic Arrays.'' Ch. 3 in Mathematical Diversions. New York: Dover, pp. 23-34, 1975.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 86, 1979.

Sloane, N. J. A. Sequences A027441 and A006003/M3849 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.