|
|
|
|
The Hypercube in ![]() is called a tesseract. It has the Schläfli Symbol
is called a tesseract. It has the Schläfli Symbol ![]() , and Vertices
, and Vertices
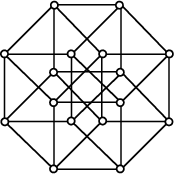
![]() . The above figures show two
visualizations of the tesseract. The figure on the left is a projection of the tesseract in 3-space (Gardner
1977), and the figure on the right is the Graph of the tesseract symmetrically
projected into the Plane (Coxeter 1973). A tesseract has 16 Vertices, 32
Edges, 24 Squares, and 8 Cubes.
. The above figures show two
visualizations of the tesseract. The figure on the left is a projection of the tesseract in 3-space (Gardner
1977), and the figure on the right is the Graph of the tesseract symmetrically
projected into the Plane (Coxeter 1973). A tesseract has 16 Vertices, 32
Edges, 24 Squares, and 8 Cubes.
See also Hypercube, Polytope
References
Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 123, 1973.
Gardner, M. ``Hypercubes.'' Ch. 4 in
Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American.
New York: Vintage Books, 1977.
Geometry Center. ``The Tesseract (or Hypercube).''
http://www.geom.umn.edu/docs/outreach/4-cube/.