|
|
|

|
A Curve of Constant Width constructed by drawing arcs from each Vertex of an Equilateral Triangle between the other two Vertices. It is the basis for the Harry Watt square drill bit. It has the smallest Area for a given width of any Curve of Constant Width.
The Area of each meniscus-shaped portion is
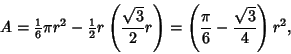 |
(1) |
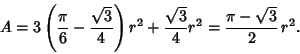 |
(2) |
| (3) |
See also Curve of Constant Width, Flower of Life, Piecewise Circular Curve, Reuleaux Polygon
References
Bogomolny, A. ``Shapes of Constant Width.''
http://www.cut-the-knot.com/do_you_know/cwidth.html.
Eppstein, D. ``Reuleaux Triangles.''
http://www.ics.uci.edu/~eppstein/junkyard/reuleaux.html.
Reuleaux, F. The Kinematics of Machinery. New York: Dover, 1963.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 52-54 and 381-383, 1991.
Yaglom, I. M. and Boltyansky, B. G. Convex Shapes. Moscow: Nauka, 1951.