Let 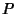 ,
, 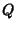 be Positive Integers. The Roots of
be Positive Integers. The Roots of
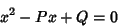 |
(1) |
are
where
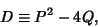 |
(4) |
so
Then define
The first few values are therefore
The sequences
are called Lucas sequences, where the definition is usually extended to include
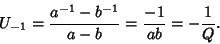 |
(16) |
For 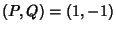 , the
, the 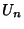 are the Fibonacci Numbers and
are the Fibonacci Numbers and 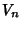 are the Lucas
Numbers. For
are the Lucas
Numbers. For 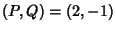 , the Pell Numbers and Pell-Lucas numbers are obtained.
, the Pell Numbers and Pell-Lucas numbers are obtained.
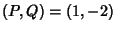 produces the Jacobsthal Numbers and Pell-Jacobsthal Numbers.
produces the Jacobsthal Numbers and Pell-Jacobsthal Numbers.
The Lucas sequences satisfy the general Recurrence Relations
Taking 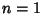 then gives
then gives
Other identities include
These formulas allow calculations for large 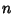 to be decomposed into a chain in which only four quantities must be kept track of
at a time, and the number of steps needed is
to be decomposed into a chain in which only four quantities must be kept track of
at a time, and the number of steps needed is 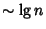 . The chain is particularly simple if
. The chain is particularly simple if 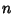 has many 2s in its
factorization.
has many 2s in its
factorization.
The 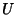 s in a Lucas sequence satisfy the Congruence
s in a Lucas sequence satisfy the Congruence
![\begin{displaymath}
U_{p^{n-1}[p-(D/p)]}\equiv 0\ \left({{\rm mod\ } {p^n}}\right)
\end{displaymath}](l2_1182.gif) |
(25) |
if
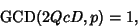 |
(26) |
where
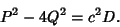 |
(27) |
This fact is used in the proof of the general Lucas-Lehmer Test.
See also Fibonacci Number, Jacobsthal Number, Lucas-Lehmer Test, Lucas Number, Lucas Polynomial
Sequence, Pell Number, Recurrence Sequence, Sylvester Cyclotomic Number
References
Dickson, L. E. ``Recurring Series; Lucas'  ,
,  .'' Ch. 17 in
History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 393-411, 1952.
.'' Ch. 17 in
History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 393-411, 1952.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, pp. 35-53, 1991.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
, ![]() be Positive Integers. The Roots of
be Positive Integers. The Roots of
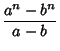
![]() , the
, the ![]() are the Fibonacci Numbers and
are the Fibonacci Numbers and ![]() are the Lucas
Numbers. For
are the Lucas
Numbers. For ![]() , the Pell Numbers and Pell-Lucas numbers are obtained.
, the Pell Numbers and Pell-Lucas numbers are obtained.
![]() produces the Jacobsthal Numbers and Pell-Jacobsthal Numbers.
produces the Jacobsthal Numbers and Pell-Jacobsthal Numbers.
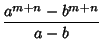
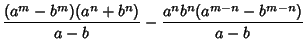
![]() s in a Lucas sequence satisfy the Congruence
s in a Lucas sequence satisfy the Congruence
![]() ,
, ![]() .'' Ch. 17 in
History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 393-411, 1952.
.'' Ch. 17 in
History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 393-411, 1952.