|
|
|
A Mersenne Number ![]() is prime Iff
is prime Iff ![]() divides
divides ![]() , where
, where
![]() and
and
| (1) |
A generalized version of the Lucas-Lehmer test lets
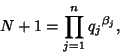 |
(2) |
| (3) |
| (4) |
See also Lucas Sequence, Mersenne Number, Rabin-Miller Strong Pseudoprime Test
References
Sloane, N. J. A. Sequence
A003010/M3494
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.