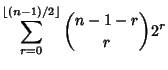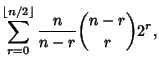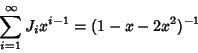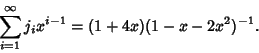The Jacobsthal numbers are the numbers obtained by the 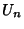 s in the Lucas Sequence with
s in the Lucas Sequence with 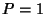 and
and 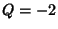 ,
corresponding to
,
corresponding to 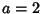 and
and 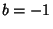 . They and the Jacobsthal-Lucas numbers (the
. They and the Jacobsthal-Lucas numbers (the 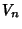 s) satisfy the Recurrence Relation
s) satisfy the Recurrence Relation
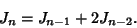 |
(1) |
The Jacobsthal numbers satisfy 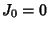 and
and 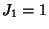 and are 0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, ... (Sloane's A001045).
The Jacobsthal-Lucas numbers satisfy
and are 0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, ... (Sloane's A001045).
The Jacobsthal-Lucas numbers satisfy 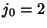 and
and 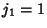 and are 2, 1, 5, 7, 17, 31, 65, 127, 257, 511, 1025, ...
(Sloane's A014551). The properties of these numbers are summarized in Horadam (1996). They are given by the closed form
expressions
and are 2, 1, 5, 7, 17, 31, 65, 127, 257, 511, 1025, ...
(Sloane's A014551). The properties of these numbers are summarized in Horadam (1996). They are given by the closed form
expressions
where
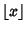 is the Floor Function and
is the Floor Function and 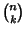 is a Binomial Coefficient. The Binet forms are
is a Binomial Coefficient. The Binet forms are
The Generating Functions are
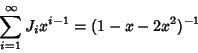 |
(6) |
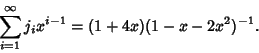 |
(7) |
The Simson Formulas are
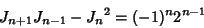 |
(8) |
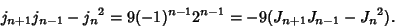 |
(9) |
Summation Formulas include
Interrelationships are
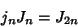 |
(12) |
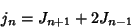 |
(13) |
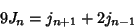 |
(14) |
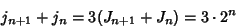 |
(15) |
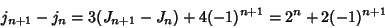 |
(16) |
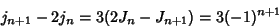 |
(17) |
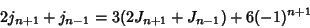 |
(18) |
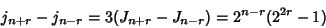 |
(21) |
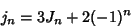 |
(22) |
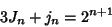 |
(23) |
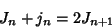 |
(24) |
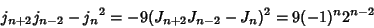 |
(25) |
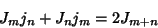 |
(26) |
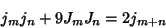 |
(27) |
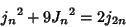 |
(28) |
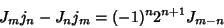 |
(29) |
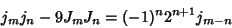 |
(30) |
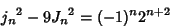 |
(31) |
(Horadam 1996).
References
Horadam, A. F. ``Jacobsthal and Pell Curves.'' Fib. Quart. 26, 79-83, 1988.
Horadam, A. F. ``Jacobsthal Representation Numbers.'' Fib. Quart. 34, 40-54, 1996.
Sloane, N. J. A. Sequences
A014551 and
A001045/M2482
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() s in the Lucas Sequence with
s in the Lucas Sequence with ![]() and
and ![]() ,
corresponding to
,
corresponding to ![]() and
and ![]() . They and the Jacobsthal-Lucas numbers (the
. They and the Jacobsthal-Lucas numbers (the ![]() s) satisfy the Recurrence Relation
s) satisfy the Recurrence Relation