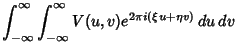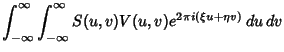From the van Cittert-Zernicke theorem,  the relationship between observed
visibility function
the relationship between observed
visibility function 
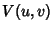 and source brightness
and source brightness 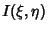 in
synthesis imaging
in
synthesis imaging  is given by
is given by
But the visibility function  is sampled only at discrete points
is sampled only at discrete points 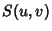 (finite sampling),
so only an approximation to
(finite sampling),
so only an approximation to 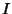 , called the ``dirty map'' and denoted
, called the ``dirty map'' and denoted 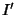 , is measured. It is given by
, is measured. It is given by
where 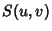 is the sampling function and
is the sampling function and 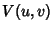 is the observed
visibility function.
is the observed
visibility function.  Let
Let 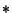 denote Convolution and rearrange the Convolution Theorem,
denote Convolution and rearrange the Convolution Theorem,
![\begin{displaymath}
{\mathcal F}[f*g]={\mathcal F}[f]{\mathcal F}[g]
\end{displaymath}](d2_557.gif) |
(3) |
into the form
![\begin{displaymath}
{\mathcal F}[{\mathcal F}^{-1}[f]*{\mathcal F}^{-1}[g]]=fg,
\end{displaymath}](d2_558.gif) |
(4) |
from which it follows that
![\begin{displaymath}
{\mathcal F}^{-1}[f]*{\mathcal F}^{-1}[g]={\mathcal F}^{-1}[fg].
\end{displaymath}](d2_559.gif) |
(5) |
Now note that
![\begin{displaymath}
I = {\mathcal F}^{-1}[V]
\end{displaymath}](d2_560.gif) |
(6) |
is the CLEAN Map, and define the ``Dirty Beam'' as the inverse Fourier Transform of the sampling function,
![\begin{displaymath}
b'\equiv {\mathcal F}^{-1}[S].
\end{displaymath}](d2_561.gif) |
(7) |
The dirty map is then given by
![\begin{displaymath}
I' = {\mathcal F}^{-1}[VS] = {\mathcal F}^{-1}[V]*{\mathcal F}^{-1}[S] = I*b'.
\end{displaymath}](d2_562.gif) |
(8) |
In order to deconvolve the desired CLEAN Map 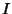 from the measured dirty map
from the measured dirty map 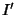 and the known Dirty Beam
and the known Dirty Beam
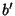 , the CLEAN Algorithm is often used.
, the CLEAN Algorithm is often used.
See also CLEAN Algorithm, CLEAN Map, Dirty Beam
© 1996-9 Eric W. Weisstein
1999-05-24
![]() the relationship between observed
visibility function
the relationship between observed
visibility function ![]()
![]() and source brightness
and source brightness ![]() in
synthesis imaging
in
synthesis imaging ![]() is given by
is given by