The Fourier Transform of the 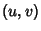 sampling distribution in synthesis imaging
sampling distribution in synthesis imaging 
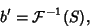 |
(1) |
also called the Synthesized Beam. It is called a ``beam'' by way of analogy with the Dirty Map
where 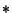 denotes Convolution. Here,
denotes Convolution. Here,  is the intensity which would be observed for an extended source by an
antenna with response pattern
is the intensity which would be observed for an extended source by an
antenna with response pattern 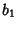 ,
,
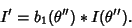 |
(3) |
The dirty beam is often a complicated function. In order to avoid introducing any high spatial frequency features when
CLEANing, an elliptical Gaussian is usually fit to the dirty beam, producing a CLEAN
Beam which is Convolved with the final iteration.
See also CLEAN Algorithm, CLEAN Map, Dirty Map
© 1996-9 Eric W. Weisstein
1999-05-24
![]() sampling distribution in synthesis imaging
sampling distribution in synthesis imaging ![]()