|
|
|
Let ![]() and
and ![]() be arbitrary functions of time
be arbitrary functions of time ![]() with Fourier Transforms. Take
with Fourier Transforms. Take
| (1) |
| (2) |
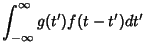 |
|||
![$\displaystyle \int_{-\infty}^\infty g(t')\left[{\int_{-\infty}^\infty F(\nu)e^{2\pi i\nu(t-t')} \,d\nu}\right]\,dt'.$](c3_59.gif) |
(3) |
![$\displaystyle \int_{-\infty}^\infty F(\nu)\left[{\int_{-\infty}^\infty g(t')e^{-2\pi i\nu t'}\,dt'}\right]e^{2\pi i\nu t}\,d\nu$](c3_60.gif) |
|||
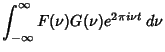 |
|||
| (4) |
| (5) |
| (6) | |||
| (7) | |||
| (8) |
See also Autocorrelation, Convolution, Fourier Transform, Wiener-Khintchine Theorem
References
Arfken, G. ``Convolution Theorem.'' §15.5 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 810-814, 1985.
Bracewell, R. ``Convolution Theorem.'' The Fourier Transform and Its Applications. New York: McGraw-Hill, pp. 108-112, 1965.
|
|
|
© 1996-9 Eric W. Weisstein