|
|
|

The curves, also called Cassini Ellipses, described by a point such that the product of its distances from two fixed
points a distance ![]() apart is a constant
apart is a constant ![]() . The shape of the curve depends on
. The shape of the curve depends on ![]() . If
. If ![]() , the curve is a single
loop with an Oval (left figure above) or dog bone (second figure) shape. The case
, the curve is a single
loop with an Oval (left figure above) or dog bone (second figure) shape. The case ![]() produces a Lemniscate
(third figure). If
produces a Lemniscate
(third figure). If ![]() , then the curve consists of two loops (right figure). The curve was first investigated by
Cassini
, then the curve consists of two loops (right figure). The curve was first investigated by
Cassini ![]() in 1680 when he was studying the relative motions of the Earth
in 1680 when he was studying the relative motions of the Earth ![]() and the Sun.
and the Sun. ![]() Cassini believed that the Sun traveled around the Earth on one of these ovals, with the Earth at one Focus of the oval.
Cassini believed that the Sun traveled around the Earth on one of these ovals, with the Earth at one Focus of the oval.
Cassini ovals are Anallagmatic Curves. The Cassini ovals are defined in two-center
Bipolar Coordinates by the equation
| (1) |
The Cassini ovals have the Cartesian equation
| (2) |
| (3) |
| (4) |
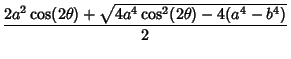 |
|||
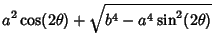 |
|||
![$\displaystyle a^2\left[{\cos(2\theta)+\sqrt{\left({b\over a}\right)^4-\sin^2(2\theta)}\,}\right].$](c1_376.gif) |
(5) |
If ![]() , the curve has Area
, the curve has Area
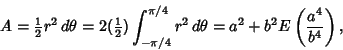 |
(6) |
| (7) |
| (8) |
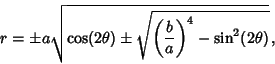 |
(9) |
![\begin{displaymath}
\theta_0\equiv {\textstyle{1\over 2}}\sin^{-1}\left[{\left({b\over a}\right)^2}\right].
\end{displaymath}](c1_386.gif) |
(10) |
See also Cassini Surface, Lemniscate, Mandelbrot Set, Oval
References
Gray, A. ``Cassinian Ovals.'' §4.2 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 63-65, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 153-155, 1972.
Lee, X. ``Cassinian Oval.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/CassinianOval_dir/cassinianOval.html
Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, pp. 187-188, 1967.
MacTutor History of Mathematics Archive. ``Cassinian Ovals.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Cassinian.html.
Yates, R. C. ``Cassinian Curves.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 8-11, 1952.
|
|
|
© 1996-9 Eric W. Weisstein