|
|
|
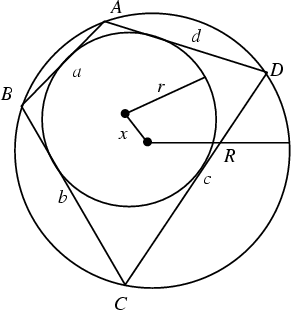
A Polygon which has both a Circumcircle (which touches each vertex) and an Incircle (which is tangent
to each side). All Triangles are bicentric with
| (1) |
| (2) |
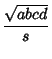 |
(3) | ||
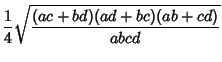 |
(4) |
| (5) |
| (6) |
| (7) |
See also Poncelet's Closure Theorem
References
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 124, 1987.
Dörrie, H. ``Fuss' Problem of the Chord-Tangent Quadrilateral.'' §39 in
100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 188-193, 1965.
|
|
|
© 1996-9 Eric W. Weisstein