|
|
|
There are two completely different definitions of the so-called Apollonius circles:
Given one side of a Triangle and the ratio of the lengths of the other two sides, the Locus of the third Vertex is the Apollonius circle (of the first type) whose Center is on the extension of the given side. For a given Triangle, there are three circles of Apollonius.
Denote the three Apollonius circles (of the first type) of a Triangle by ![]() ,
, ![]() , and
, and ![]() , and their centers
, and their centers
![]() ,
, ![]() , and
, and ![]() . The center
. The center ![]() is the intersection of the side
is the intersection of the side ![]() with the tangent to the Circumcircle
at
with the tangent to the Circumcircle
at ![]() .
. ![]() is also the pole of the Symmedian Point
is also the pole of the Symmedian Point ![]() with respect to Circumcircle. The centers
with respect to Circumcircle. The centers ![]() ,
,
![]() , and
, and ![]() are Collinear on the Polar of
are Collinear on the Polar of ![]() with regard to its Circumcircle, called the
Lemoine Line. The circle of Apollonius
with regard to its Circumcircle, called the
Lemoine Line. The circle of Apollonius ![]() is also the locus of a point whose Pedal Triangle is
Isosceles such that
is also the locus of a point whose Pedal Triangle is
Isosceles such that
![]() .
.
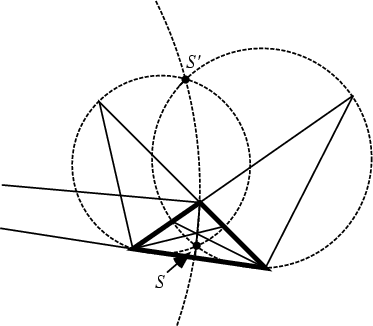
Let ![]() and
and ![]() be points on the side line
be points on the side line ![]() of a Triangle
of a Triangle ![]() met by the interior and exterior
Angle Bisectors of Angles
met by the interior and exterior
Angle Bisectors of Angles ![]() . The Circle with Diameter
. The Circle with Diameter ![]() is
called the
is
called the ![]() -Apollonian circle. Similarly, construct the
-Apollonian circle. Similarly, construct the ![]() - and
- and ![]() -Apollonian circles. The Apollonian circles pass
through the Vertices
-Apollonian circles. The Apollonian circles pass
through the Vertices ![]() ,
, ![]() , and
, and ![]() , and through the two Isodynamic Points
, and through the two Isodynamic Points ![]() and
and ![]() .
The Vertices of the D-Triangle lie on the respective Apollonius circles.
.
The Vertices of the D-Triangle lie on the respective Apollonius circles.
See also Apollonius' Problem, Apollonius Pursuit Problem, Casey's Theorem, Hart's Theorem, Isodynamic Points, Soddy Circles
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 40 and 294-299, 1929.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 14-23, 1990.
|
|
|
© 1996-9 Eric W. Weisstein