|
|
|
A function (also called a Tapering Function) used to bring an interferogram smoothly down to zero at the edges of the sampled region. This suppresses sidelobes which would otherwise be produced, but at the expense of widening the lines and therefore decreasing the resolution.
The following are apodization functions for symmetrical (2-sided) interferograms, together with the Instrument
Functions (or Apparatus Functions) they produce and a blowup of the
Instrument Function sidelobes. The Instrument Function ![]() corresponding to a given apodization function
corresponding to a given apodization function
![]() can be computed by taking the finite Fourier Cosine Transform,
can be computed by taking the finite Fourier Cosine Transform,
| (1) |

| Type | Apodization Function | Instrument Function |
| Bartlett |
|
|
| Blackman | ||
| Connes |
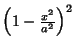 |
|
| Cosine |
|
|
| Gaussian |
|
|
| Hamming | ||
| Hanning | ||
| Uniform | 1 |
|
| Welch |
|
where
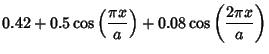 |
(2) | ||
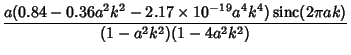 |
(3) | ||
| (4) | |||
| (5) | |||
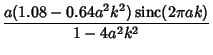 |
(6) | ||
| (7) | |||
| (8) | |||
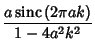 |
(9) | ||
| (10) | |||
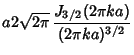 |
(11) | ||
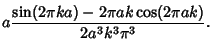 |
(12) |
| Type | Instrument Function FWHM | IF Peak |
|
|
| Bartlett | 1.77179 | 1 | 0.00000000 | |
| Blackman | 2.29880 | 0.84 | 0.00124325 | |
| Connes | 1.90416 |
|
||
| Cosine | 1.63941 |
|
||
| Gaussian | -- | 1 | -- | -- |
| Hamming | 1.81522 | 1.08 | 0.00734934 | |
| Hanning | 2.00000 | 1 | 0.00843441 | |
| Uniform | 1.20671 | 2 | ||
| Welch | 1.59044 |
|
A general symmetric apodization function ![]() can be written as a Fourier Series
can be written as a Fourier Series
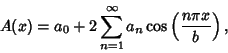 |
(13) |
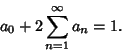 |
(14) |
|
|
|
|
|
(15) |
| (16) |
| (17) |
| (18) |
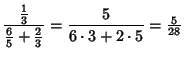 |
(19) | ||
| (20) |
| (21) | |||
| (22) |
| (23) | |||
| (24) | |||
| (25) |
See also Bartlett Function, Blackman Function, Connes Function, Cosine Apodization Function, Full Width at Half Maximum, Gaussian Function, Hamming Function, Hann Function, Hanning Function, Mertz Apodization Function, Parzen Apodization Function, Uniform Apodization Function, Welch Apodization Function
References
Ball, J. A. ``The Spectral Resolution in a Correlator System'' §4.3.5 in Methods of Experimental Physics
12C (Ed. M. L. Meeks). New York: Academic Press, pp. 55-57, 1976.
Blackman, R. B. and Tukey, J. W. ``Particular Pairs of Windows.'' In The Measurement of Power Spectra, From the
Point of View of Communications Engineering. New York: Dover, pp. 95-101, 1959.
Brault, J. W. ``Fourier Transform Spectrometry.'' In High Resolution in Astronomy: 15th Advanced Course of the
Swiss Society of Astronomy and Astrophysics (Ed. A. Benz, M. Huber, and M. Mayor). Geneva Observatory, Sauverny,
Switzerland, pp. 31-32, 1985.
Harris, F. J. ``On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform.''
Proc. IEEE 66, 51-83, 1978.
Norton, R. H. and Beer, R. ``New Apodizing Functions for Fourier Spectroscopy.'' J. Opt. Soc. Amer. 66,
259-264, 1976.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed.
Cambridge, England: Cambridge University Press, pp. 547-548, 1992.
Schnopper, H. W. and Thompson, R. I. ``Fourier Spectrometers.'' In Methods of Experimental Physics 12A
(Ed. M. L. Meeks). New York: Academic Press, pp. 491-529, 1974.
|
|
|
© 1996-9 Eric W. Weisstein