|
|
|
![$\sum_{k=0}^n q^{k^2+ak}\left[{\matrix{2n-k+a\cr k\cr}}\right]$](a_929.gif)
|
|
![$ = \sum_{k=-\infty}^\infty q^{10k^2+(4a-1)k}\left[{\matrix{2n+2a+2\cr n-5k\cr}}\right] {[10k+2a+2]\over [2n+2a+2]},\quad$](a_930.gif)
|
(1) |
![$\sum_{k=-\left\lfloor{a/2}\right\rfloor }^n q^{k^2+2ak}\left[{\matrix{n+k+a\cr n-k\cr}}\right]$](a_933.gif)
|
|
![$ = \sum_{-\left\lfloor{(n+2a+2)/5}\right\rfloor }^{\left\lfloor{n/5}\right\rflo...
...+1)k}\left[{\matrix{2n+2a+2\cr 5-5k\cr}}\right]{[10k+2a+2]\over[2n+2a+2]},\quad$](a_934.gif)
|
(2) |
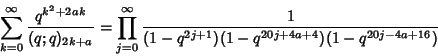 |
(3) |
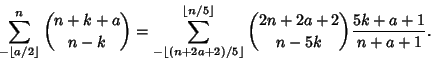 |
(4) |
References
Andrews, G. E. ``A Polynomial Identity which Implies the Rogers-Ramanujan Identities.'' Scripta Math.
28, 297-305, 1970.
Paule, P. ``Short and Easy Computer Proofs of the Rogers-Ramanujan Identities and of Identities of Similar Type.'' Electronic J. Combinatorics 1, R10 1-9, 1994.
http://www.combinatorics.org/Volume_1/volume1.html#R10.