The Jacobi triple product is the beautiful identity
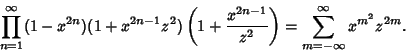 |
(1) |
In terms of the Q-Function, (1) is written
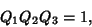 |
(2) |
which is one of the two Jacobi Identities. For the special case of 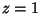 , (1) becomes
, (1) becomes
where 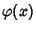 is the one-variable Ramanujan Theta Function.
is the one-variable Ramanujan Theta Function.
To prove the identity, define the function
Then
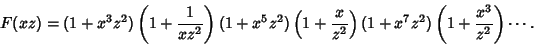 |
(5) |
Taking (5) 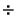 (4),
(4),
which yields the fundamental relation
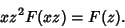 |
(7) |
Now define
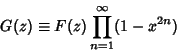 |
(8) |
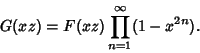 |
(9) |
Using (7), (9) becomes
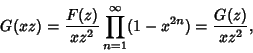 |
(10) |
so
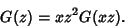 |
(11) |
Expand 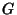 in a Laurent Series. Since
in a Laurent Series. Since 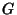 is an Even Function, the Laurent Series contains only even terms.
is an Even Function, the Laurent Series contains only even terms.
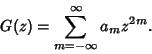 |
(12) |
Equation (11) then requires that
This can be re-indexed with  on the left side of (13)
on the left side of (13)
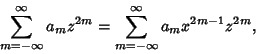 |
(14) |
which provides a Recurrence Relation
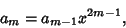 |
(15) |
so
The exponent grows greater by 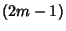 for each increase in
for each increase in 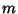 of 1. It is given by
of 1. It is given by
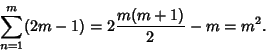 |
(19) |
Therefore,
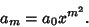 |
(20) |
This means that
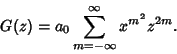 |
(21) |
The Coefficient 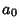 must be determined by going back to (4) and (8) and letting
must be determined by going back to (4) and (8) and letting 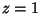 . Then
. Then
since multiplication is Associative. It is clear from this expression that the 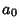 term must be 1, because all
other terms will contain higher Powers of
term must be 1, because all
other terms will contain higher Powers of 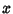 . Therefore,
. Therefore,
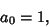 |
(24) |
so we have the Jacobi triple product,
See also Euler Identity, Jacobi Identities, Q-Function, Quintuple Product Identity,
Ramanujan Psi Sum, Ramanujan Theta Functions, Schröter's Formula, Theta
Function
References
Andrews, G. E.
 -Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.
-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.
Borwein, J. M. and Borwein, P. B. ``Jacobi's Triple Product and Some Number Theoretic Applications.'' Ch. 3 in
Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 62-101, 1987.
Jacobi, C. G. J. Fundamentia Nova Theoriae Functionum Ellipticarum. Regiomonti, Sumtibus fratrum Borntraeger, p. 90, 1829.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge
University Press, p. 470, 1990.
© 1996-9 Eric W. Weisstein
1999-05-25
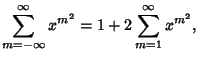
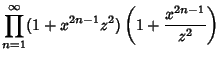
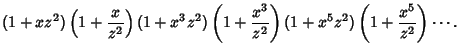
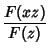
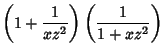
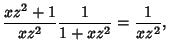
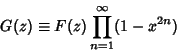
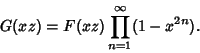
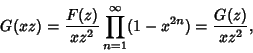
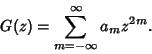
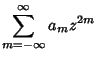
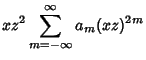
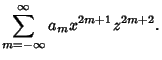
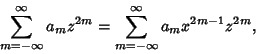
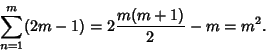
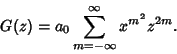
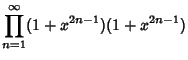
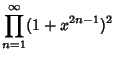
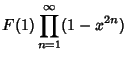
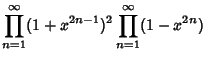
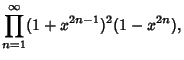
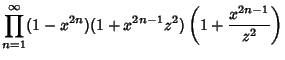
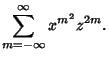
![]() -Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.
-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra.
Providence, RI: Amer. Math. Soc., pp. 63-64, 1986.