|
|
|
Let
| (1) |
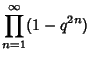 |
(2) | ||
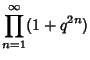 |
(3) | ||
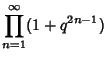 |
(4) | ||
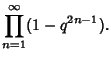 |
(5) |
| (6) | |||
| (7) | |||
| (8) | |||
| (9) |
See also Jacobi Identities, q-Series
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 55 and 63-85, 1987.
Tannery, J. and Molk, J. Elements de la Théorie des Fonctions Elliptiques, 4 vols. Paris: Gauthier-Villars et fils, 1893-1902.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge
University Press, pp. 469-473 and 488-489, 1990.