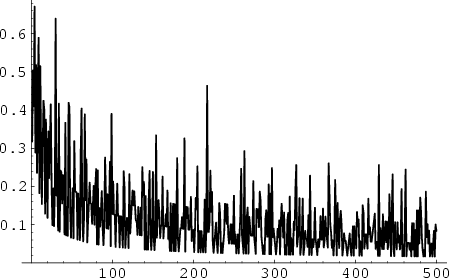
Andrica's Conjecture

Andrica's conjecture states that, for $p_n$ the $n$th Prime Number, the Inequality

$$A_n\equiv \sqrt{p_{n+1}}-\sqrt{p_n}<1$$

holds, where the discrete function $A_n$ is plotted above. The largest value among the first 1000 Primes is for $n=4$, giving $\sqrt{11}-\sqrt{7}\approx 0.670873$. Since the Andrica function falls asymptotically as $n$ increases so a Prime Gap of increasing size is needed at large $n$, it seems likely the Conjecture is true. However, it has not yet been proven.

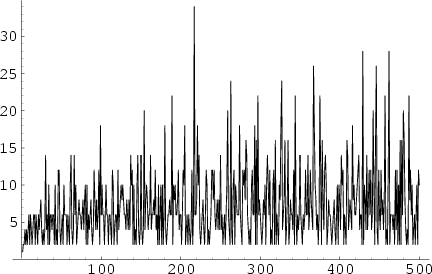
$A_n$ bears a strong resemblance to the Prime Difference Function, plotted above, the first few values of which are 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, ... (Sloane's A001223).

See also Brocard's Conjecture, Good Prime, Fortunate Prime, Pólya Conjecture, Prime Difference Function, Twin Peaks

References

Golomb, S. W. ``Problem E2506: Limits of Differences of Square Roots.'' Amer. Math. Monthly 83, 60-61, 1976.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 21, 1994.

Rivera, C. ``Problems & Puzzles (Conjectures): Andrica's Conjecture.'' http://www.sci.net.mx/~crivera/conjectures/conj_008.htm.

Sloane, N. J. A. Sequence A001223/M0296 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.