|
|
|
Also known as Bernoulli's Theorem. Let ![]() , ...,
, ..., ![]() be a sequence of independent and identically distributed
random variables, each having a Mean
be a sequence of independent and identically distributed
random variables, each having a Mean
![]() and Standard Deviation
and Standard Deviation ![]() . Define a new variable
. Define a new variable
| (1) |
| (2) |
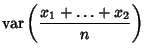 |
|||
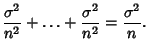 |
(3) |
| (4) |
| (5) |
Stated another way, if an event occurs ![]() times in
times in ![]() Trials and if
Trials and if ![]() is the probability of success
in a single Trial, then the probability that
is the probability of success
in a single Trial, then the probability that
![]() for
for ![]() an arbitrary Positive quantity
approaches 1 as
an arbitrary Positive quantity
approaches 1 as ![]() .
.
See also Law of Truly Large Numbers, Strong Law of Large Numbers