Weak convergence is usually either denoted
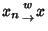 or
or
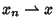 . A Sequence
. A Sequence 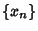 of
Vectors in an Inner Product Space
of
Vectors in an Inner Product Space 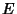 is called weakly convergent to a Vector in
is called weakly convergent to a Vector in 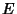 if
if
Every Strongly Convergent sequence is also weakly convergent (but the opposite does not
usually hold). This can be seen as follows. Consider the sequence 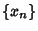 that converges strongly to
that converges strongly to 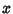 , i.e.,
, i.e.,
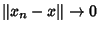 as
as
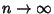 . Schwarz's Inequality now gives
. Schwarz's Inequality now gives
The definition of weak convergence is therefore satisfied.
See also Inner Product Space, Schwarz's Inequality, Strong Convergence
© 1996-9 Eric W. Weisstein
1999-05-26
![]() or
or
![]() . A Sequence
. A Sequence ![]() of
Vectors in an Inner Product Space
of
Vectors in an Inner Product Space ![]() is called weakly convergent to a Vector in
is called weakly convergent to a Vector in ![]() if
if