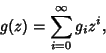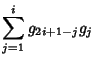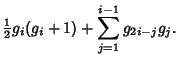N.B. A detailed on-line essay by S. Finch
was the starting point for this entry.
A Rooted Tree for which the Root is adjacent to at most two Vertices, and all nonroot Vertices are adjacent to at most three Vertices. Let 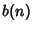 be the number of weakly binary trees of order
be the number of weakly binary trees of order 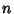 , then
, then 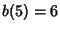 . Let
. Let
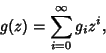 |
(1) |
where
Otter (Otter 1948, Harary and Palmer 1973, Knuth 1969) showed that
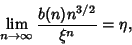 |
(6) |
where
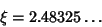 |
(7) |
is the unique Positive Root of
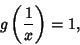 |
(8) |
and
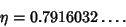 |
(9) |
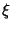 is also given by
is also given by
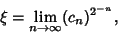 |
(10) |
where 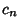 is given by
is given by
giving
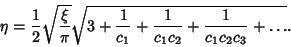 |
(13) |
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/otter/otter.html
Harary, F. Graph Theory. Reading, MA: Addison-Wesley, 1969.
Harary, F. and Palmer, E. M. Graphical Enumeration. New York: Academic Press, 1973.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1973.
Otter, R. ``The Number of Trees.'' Ann. Math. 49, 583-599, 1948.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be the number of weakly binary trees of order
be the number of weakly binary trees of order ![]() , then
, then ![]() . Let
. Let