|
|
|
The number of Permutations of ![]() objects in which no object appear in its natural place (i.e.,
so-called ``Derangements'').
objects in which no object appear in its natural place (i.e.,
so-called ``Derangements'').
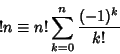 |
(1) |
| (2) |
The subfactorials are also called the Rencontres Numbers and satisfy the Recurrence
Relations
| (3) |
| (4) |
The only number equal to the sum of subfactorials of its digits is
| (5) |
See also Derangement, Factorial, Married Couples Problem, Rooks Problem, Superfactorial
References
Dörrie, H. §6 in 100 Great Problems of Elementary Mathematics: Their History and Solutions.
New York: Dover, pp. 19-21, 1965.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 167, 1979.
Sloane, N. J. A. Sequence
A000166/M1937
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in
Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, p. 67, 1997.
|
|
|
© 1996-9 Eric W. Weisstein