|
|
|
The superfactorial of ![]() is defined by Pickover (1995) as
is defined by Pickover (1995) as
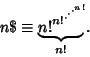
Sloane and Plouffe (1995) define the superfactorial by
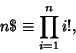
See also Factorial, G-Function, Large Number, Subfactorial
References
Pickover, C. A. Keys to Infinity. New York: Wiley, p. 102, 1995.
Sloane, N. J. A. Sequence
A000178/M2049
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.