|
|
|
A Permutation of ![]() ordered objects in which none of the objects appears in its natural place. The function
giving this quantity is the Subfactorial
ordered objects in which none of the objects appears in its natural place. The function
giving this quantity is the Subfactorial ![]() , defined by
, defined by
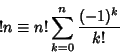 |
(1) |
| (2) |
| (3) |
| (4) |
See also Married Couples Problem, Permutation, Root, Subfactorial
References
Aitken, A. C. Determinants and Matrices. Westport, CT: Greenwood Pub., p. 135, 1983.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, pp. 46-47, 1987.
Coolidge, J. L. An Introduction to Mathematical Probability. Oxford, England: Oxford University Press, p. 24, 1925.
Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 115-116, 1996.
de Montmort, P. R. Essai d'analyse sur les jeux de hasard. Paris, p. 132, 1713.
Dickau, R. M. ``Derangements.''
http://forum.swarthmore.edu/advanced/robertd/derangements.html.
Durell, C. V. and Robson, A. Advanced Algebra. London, p. 459, 1937.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, 1996.
Roberts, F. S. Applied Combinatorics. Englewood Cliffs, NJ: Prentice-Hall, 1984.
Ruskey, F. ``Information on Derangements.''
http://sue.csc.uvic.ca/~cos/inf/perm/Derangements.html.
Sloane, N. J. A. Sequence
A000166/M1937
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Stanley, R. P. Enumerative Combinatorics, Vol. 1. New York: Cambridge University Press, p. 67, 1986.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 123, 1991.
|
|
|
© 1996-9 Eric W. Weisstein