|
|
|
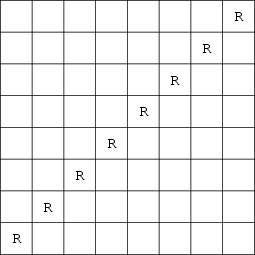
The rook is a Chess piece which may move any number of spaces either horizontally or vertically per move. The
maximum number of nonattacking rooks which may be placed on an ![]() Chessboard is
Chessboard is ![]() . This arrangement is
achieved by placing the rooks along the diagonal (Madachy 1979). The total number of ways of placing
. This arrangement is
achieved by placing the rooks along the diagonal (Madachy 1979). The total number of ways of placing ![]() nonattacking
rooks on an
nonattacking
rooks on an ![]() board is
board is ![]() (Madachy 1979, p. 47). The number of rotationally and reflectively inequivalent
ways of placing
(Madachy 1979, p. 47). The number of rotationally and reflectively inequivalent
ways of placing ![]() nonattacking rooks on an
nonattacking rooks on an ![]() board are 1, 2, 7, 23, 115, 694, ... (Sloane's A000903; Dudeney 1970, p. 96;
Madachy 1979, pp. 46-54).
board are 1, 2, 7, 23, 115, 694, ... (Sloane's A000903; Dudeney 1970, p. 96;
Madachy 1979, pp. 46-54).
The minimum number of rooks needed to occupy or attack all spaces on an ![]() Chessboard is 8 (Madachy 1979),
arranged in the same orientation as above.
Chessboard is 8 (Madachy 1979),
arranged in the same orientation as above.
Consider an ![]() chessboard with the restriction that, for every subset of
chessboard with the restriction that, for every subset of
![]() , a rook may not be put in
column
, a rook may not be put in
column ![]() (mod
(mod ![]() ) when on row
) when on row ![]() , where the rows are numbered 0, 1, ...,
, where the rows are numbered 0, 1, ..., ![]() . Vardi (1991) denotes the number of
rook solutions so restricted as
. Vardi (1991) denotes the number of
rook solutions so restricted as
![]() .
.
![]() is simply the number of
Derangements on
is simply the number of
Derangements on ![]() symbols, known as a Subfactorial. The first few values are 1, 2, 9, 44,
265, 1854, ... (Sloane's A000166).
symbols, known as a Subfactorial. The first few values are 1, 2, 9, 44,
265, 1854, ... (Sloane's A000166).
![]() is a solution to the Married Couples Problem,
sometimes known as Ménage Numbers. The first few Ménage Numbers are
is a solution to the Married Couples Problem,
sometimes known as Ménage Numbers. The first few Ménage Numbers are
![]() , 1, 0, 2, 13, 80, 579, ... (Sloane's A000179).
, 1, 0, 2, 13, 80, 579, ... (Sloane's A000179).
Although simple formulas are not known for general ![]() , ...,
, ..., ![]() , Recurrence Relations
can be used to compute
, Recurrence Relations
can be used to compute
![]() in polynomial time for
in polynomial time for ![]() , ..., 6 (Metropolis et al.
1969, Minc 1978, Vardi 1991).
, ..., 6 (Metropolis et al.
1969, Minc 1978, Vardi 1991).
See also Chess, Ménage Number, Rook Number, Rook Reciprocity Theorem
References
Dudeney, H. E. ``The Eight Rooks.'' §295 in Amusements in Mathematics. New York: Dover, p. 88, 1970.
Kraitchik, M. ``The Problem of the Rooks'' and ``Domination of the Chessboard.'' §10.2 and 10.4 in
Mathematical Recreations. New York: W. W. Norton, pp. 240-247 and 255-256, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 36-37, 1979.
Metropolis, M.; Stein, M. L.; and Stein, P. R. ``Permanents of Cyclic (0, 1) Matrices.'' J. Combin. Th.
7, 291-321, 1969.
Minc, H. §3.1 in Permanents. Reading, MA: Addison-Wesley, 1978.
Riordan, J. Chs. 7-8 in An Introduction to Combinatorial Analysis. Princeton, NJ: Princeton University Press, 1978.
Sloane, N. J. A. Sequences
A000903/M1761
A000166/M1937, and
A000179/M2062
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 123-124, 1991.
|
|
|
© 1996-9 Eric W. Weisstein