|
|
|
A Separating Family is a Set of Subsets in which each pair of adjacent elements are found separated,
each in one of two disjoint subsets. The 26 letters of the alphabet can be separated by a family of 9,
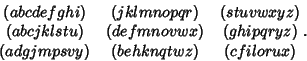
See also Katona's Problem
References
Honsberger, R. ``Cai Mao-Cheng's Solution to Katona's Problem on Families of Separating Subsets.'' Ch. 18 in
Mathematical Gems III. Washington, DC: Math. Assoc. Amer.,
pp. 224-239, 1985.
Sloane, N. J. A. Sequence
A007600/M0456
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.