Katona's Problem

Find the minimum number $f(n)$ of subsets in a Separating Family for a Set of $n$ elements, where a Separating Family is a Set of Subsets in which each pair of adjacent elements is found separated, each in one of two disjoint subsets. For example, the 26 letters of the alphabet can be separated by a family of nine:

$$\matrix{ (abcdefghi) & (jklmnopqr) & (stuvwxyz)\cr (abcjklst... ...x) & (ghipqryz)\cr (adgjmpsvy) & (behknqtwz) & (cfilorux)\cr}.$$

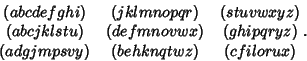
The problem was posed by Katona (1973) and solved by C. Mao-Cheng in 1982,

$$f(n)=\min\left\{{2p+3\left\lceil{\log_3\left({n\over 2^p}\right)}\right\rceil : p=0, 1, 2}\right\},$$

where $\left\lceil{x}\right\rceil$ is the Ceiling Function. $f(n)$ is nondecreasing, and the values for $n=1$, 2, ... are 0, 2, 3, 4, 5, 5, 6, 6, 6, 7, ... (Sloane's A007600). The values at which $f(n)$ increases are 1, 2, 3, 4, 5, 7, 10, 13, 19, 28, 37, ... (Sloane's A007601), so $f(26)=9$, as illustrated in the preceding example.

See also Separating Family

References

Honsberger, R. ``Cai Mao-Cheng's Solution to Katona's Problem on Families of Separating Subsets.'' Ch. 18 in Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 224-239, 1985.

Katona, G. O. H. ``Combinatorial Search Problem.'' In A Survey of Combinatorial Theory (Ed. J. N. Srivasta et al.). Amsterdam, Netherlands: North-Holland, pp. 285-308, 1973.

Sloane, N. J. A. Sequences A007600/M0456 and A007601/M0525 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.