A semi-oriented 2-variable Knot Polynomial defined by
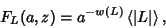 |
(1) |
where 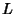 is an oriented Link Diagram,
is an oriented Link Diagram, 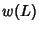 is the Writhe of
is the Writhe of 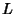 ,
, 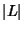 is the unoriented diagram
corresponding to
is the unoriented diagram
corresponding to 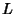 , and
, and
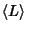 is the Bracket Polynomial. It was developed by Kauffman by extending the
BLM/Ho Polynomial
is the Bracket Polynomial. It was developed by Kauffman by extending the
BLM/Ho Polynomial 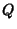 to two variables, and satisfies
to two variables, and satisfies
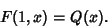 |
(2) |
The Kauffman Polynomial is a generalization of the Jones Polynomial 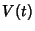 since it satisfies
since it satisfies
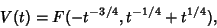 |
(3) |
but its relationship to the HOMFLY Polynomial is not well understood. In general, it has more terms than the
HOMFLY Polynomial, and is therefore more powerful for discriminating Knots. It is a semi-oriented
Polynomial because changing the orientation only changes 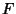 by a Power of
by a Power of 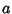 . In particular, suppose
. In particular, suppose 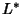 is obtained from
is obtained from 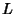 by reversing the orientation of component
by reversing the orientation of component 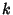 , then
, then
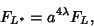 |
(4) |
where 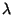 is the Linking Number of
is the Linking Number of 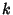 with
with 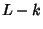 (Lickorish and Millett 1988).
(Lickorish and Millett 1988). 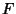 is unchanged by
Mutation.
is unchanged by
Mutation.
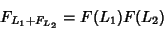 |
(5) |
![\begin{displaymath}
F_{L_1\cup L_2}=[(a^{-1}+a)x^{-1}-1]F_{L_1}F_{L_2}.
\end{displaymath}](k_337.gif) |
(6) |
M. B. Thistlethwaite has tabulated the Kauffman 2-variable Polynomial for Knots up to 13 crossings.
References
Lickorish, W. B. R. and Millett, B. R. ``The New Polynomial Invariants of Knots and Links.'' Math. Mag. 61, 1-23, 1988.
Stoimenow, A. ``Kauffman Polynomials.'' http://www.informatik.hu-berlin.de/~stoimeno/ptab/k10.html.
 Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.