Also called the Twist Number. The sum of crossings 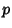 of a Link
of a Link 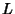 ,
,
where 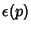 defined to be
defined to be 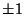 if the overpass slants from top left to bottom right or bottom left to top
right and
if the overpass slants from top left to bottom right or bottom left to top
right and 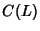 is the set of crossings of an oriented Link. If a Knot
is the set of crossings of an oriented Link. If a Knot 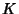 is Amphichiral, then
is Amphichiral, then
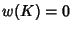 (Thistlethwaite). Letting Lk be the Linking Number of the two components of a ribbon, Tw be the
Twist, and Wr be the writhe, then
(Thistlethwaite). Letting Lk be the Linking Number of the two components of a ribbon, Tw be the
Twist, and Wr be the writhe, then
(Adams 1994, p. 187).
See also Screw, Twist
References
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York:
W. H. Freeman, 1994.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() of a Link
of a Link ![]() ,
,