|
|
|
A set is a Finite or Infinite collection of objects. Older words for set include Aggregate and
Class. Russell also uses the term Manifold to refer to a set. The study of sets and their
properties is the object of Set Theory. Symbols used to operate on sets include ![]() (which denotes the
Empty Set
(which denotes the
Empty Set ![]() ),
), ![]() (which denotes the Power Set of a set),
(which denotes the Power Set of a set), ![]() (which means ``and'' or
Intersection), and
(which means ``and'' or
Intersection), and ![]() (which means ``or'' or Union).
(which means ``or'' or Union).
The Notation ![]() , where
, where ![]() and
and ![]() are arbitrary sets, is used to denote the set of Maps from
are arbitrary sets, is used to denote the set of Maps from ![]() to
to
![]() . For example, an element of
. For example, an element of ![]() would be a Map from the Natural Numbers
would be a Map from the Natural Numbers
![]() to the set
to the set ![]() . Call such a function
. Call such a function ![]() , then
, then ![]() ,
, ![]() , etc., are elements of
, etc., are elements of ![]() , so call them
, so call them ![]() ,
, ![]() ,
etc. This now looks like a Sequence of elements of
,
etc. This now looks like a Sequence of elements of ![]() , so sequences are really just functions from
, so sequences are really just functions from ![]() to
to ![]() .
This Notation is standard in mathematics and is frequently used in symbolic dynamics to denote sequence spaces.
.
This Notation is standard in mathematics and is frequently used in symbolic dynamics to denote sequence spaces.
Let ![]() ,
, ![]() , and
, and ![]() be sets. Then operation on these sets using the
be sets. Then operation on these sets using the ![]() and
and ![]() operators is Commutative
operators is Commutative
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
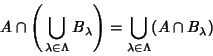 |
(7) |
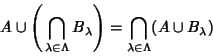 |
(8) |
The table below gives symbols for some common sets in mathematics.
| Symbol | Set |
| Complex Numbers | |
| Quaternions | |
| Integers | |
| Natural Numbers | |
| Rational Numbers | |
| Real Numbers in |
|
| Integers | |
| integers (mod |
|
| Negative Integers | |
| Positive Integers | |
| Nonnegative Integers |
See also Aggregate, Analytic Set, Borel Set, C, Class (Set), Coanalytic Set, Definable Set, Derived Set, Double-Free Set, Extension, Ground Set, I, Intension, Intersection, Kinney's Set, Manifold, N, Perfect Set, Poset, Q, R, Set Difference, Set Theory, Triple-Free Set, Union, Venn Diagram, Well-Ordered Set, Z, Z-, Z+
References
Courant, R. and Robbins, H. ``The Algebra of Sets.'' Supplement to Ch. 2 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 108-116, 1996.
|
|
|
© 1996-9 Eric W. Weisstein