|
|
|
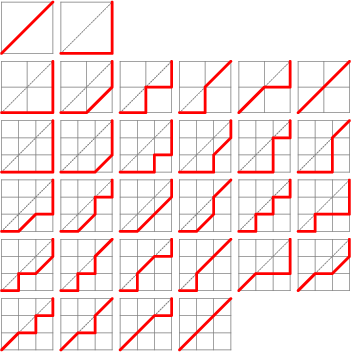
The Schröder number ![]() is the number of Lattice Paths in the Cartesian plane that start at
(0, 0), end at
is the number of Lattice Paths in the Cartesian plane that start at
(0, 0), end at ![]() , contain no points above the line
, contain no points above the line ![]() , and are composed only of steps (0, 1), (1, 0), and (1,
1), i.e.,
, and are composed only of steps (0, 1), (1, 0), and (1,
1), i.e., ![]() ,
, ![]() , and
, and ![]() . The diagrams illustrating the paths generating
. The diagrams illustrating the paths generating ![]() ,
, ![]() , and
, and ![]() are illustrated above. The numbers
are illustrated above. The numbers ![]() are given by the Recurrence Relation
are given by the Recurrence Relation
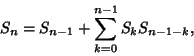
See also Binomial Coefficient, Catalan Number, Delannoy Number, Lattice Path, Motzkin Number, p-Good Path
References
Sloane, N. J. A. Sequence
A006318/M1659
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.