|
|
|
A Lattice Path from one point to another is ![]() -good if it lies completely below the line
-good if it lies completely below the line
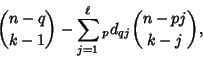
See also Catalan Number, Lattice Path, Schröder Number
References
Hilton, P. and Pederson, J. ``Catalan Numbers, Their Generalization, and Their Uses.'' Math. Intel. 13, 64-75, 1991.