|
|
|
The Delannoy numbers are defined by
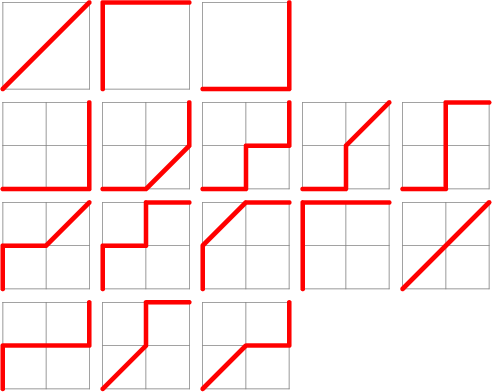
For ![]() , the Delannoy numbers are the number of ``king walks''
, the Delannoy numbers are the number of ``king walks''
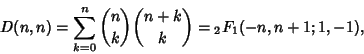
The Schröder Numbers bear the same relation to the Delannoy numbers as the Catalan Numbers do to the Binomial Coefficients.
See also Binomial Coefficient, Catalan Number, Motzkin Number, Schröder Number
References
Moser, L. ``King Paths on a Chessboard.'' Math. Gaz. 39, 54, 1955.
Sloane, N. J. A. Sequence
A001850/M2942
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, 1991.