|
|
|
A run is a sequence of more than one consecutive identical outcomes, also known as a
Clump. Given ![]() Bernoulli Trials (say, in the
form of Coin Tossings), the probability
Bernoulli Trials (say, in the
form of Coin Tossings), the probability ![]() of a run of
of a run of
![]() consecutive heads or tails is given by the Recurrence Relation
consecutive heads or tails is given by the Recurrence Relation
| (1) |
Let ![]() denote the number of sequences of
denote the number of sequences of ![]() indistinguishable objects of type
indistinguishable objects of type ![]() and
and ![]() indistinguishable
objects of type
indistinguishable
objects of type ![]() in which no
in which no ![]() -run occurs. The probability that a
-run occurs. The probability that a ![]() -run does occur is then given
by
-run does occur is then given
by
| (2) |
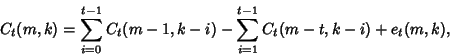 |
(3) |
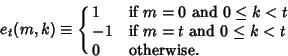 |
(4) |
|
|
|
|
|
(5) |
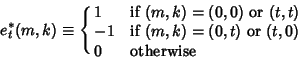 |
(6) |
Given ![]() Bernoulli Trials with a probability of success
(heads)
Bernoulli Trials with a probability of success
(heads) ![]() , the expected number of tails is
, the expected number of tails is ![]() , so the expected number of tail
runs
, so the expected number of tail
runs ![]() is
is
![]() . Continuing,
. Continuing,
| (7) |
| (8) |
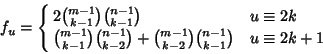 |
(9) |
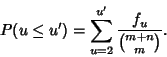 |
(10) |
Bloom (1996) gives the expected number of noncontiguous ![]() -runs in a sequence of
-runs in a sequence of ![]() 0s
and
0s
and ![]() 1s as
1s as
| (11) |
| (12) | |||
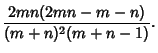 |
(13) |
See also Coin Tossing, Eulerian Number, Permutation, s-Run
References
Bloom, D. M. ``Probabilities of Clumps in a Binary Sequence (and How to Evaluate Them Without Knowing a Lot).''
Math. Mag. 69, 366-372, 1996.
Gardner, M. Aha! Gotcha: Paradoxes to Puzzle and Delight. New York: W. H. Freeman, p. 124, 1982.
Godbole, A. P. ``On Hypergeometric and Related Distributions of Order
Godbole, A. P. and Papastavnidis, G. (Eds.). Runs and Patterns in Probability: Selected Papers.
New York: Kluwer, 1994.
Gordon, L.; Schilling, M. F.; and Waterman, M. S. ``An Extreme Value Theory for Long Head Runs.''
Prob. Th. and Related Fields 72, 279-287, 1986.
Goulden, I. P. and Jackson, D. M. Combinatorial Enumeration. New York: Wiley, 1983.
Mood, A. M. ``The Distribution Theory of Runs.'' Ann. Math. Statistics 11, 367-392, 1940.
Philippou, A. N. and Makri, F. S. ``Successes, Runs, and Longest Runs.'' Stat. Prob. Let. 4, 211-215, 1986.
Schilling, M. F. ``The Longest Run of Heads.'' Coll. Math. J. 21, 196-207, 1990.
Schuster, E. F. In Runs and Patterns in Probability: Selected Papers (Ed. A. P. Godbole and S. Papastavridis).
Boston, MA: Kluwer, pp. 91-111, 1994.
![]() .'' Commun. Stat.: Th. and Meth.
19, 1291-1301, 1990.
.'' Commun. Stat.: Th. and Meth.
19, 1291-1301, 1990.
|
|
|
© 1996-9 Eric W. Weisstein