|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let ![]() be a
be a ![]() -Vector whose entries are each 1 (with probability
-Vector whose entries are each 1 (with probability ![]() ) or 0 (with probability
) or 0 (with probability ![]() ).
An
).
An ![]() -run is an isolated group of
-run is an isolated group of ![]() consecutive 1s. Ignoring the boundaries, the total number of runs
consecutive 1s. Ignoring the boundaries, the total number of runs ![]() satisfies
satisfies
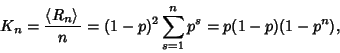
See also Percolation Theory, s-Cluster
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/rndprc/rndprc.html