|
|
|
The number of Permutations of length ![]() with
with ![]() Runs, denoted
Runs, denoted
![]() ,
, ![]() , or
, or ![]() . The Eulerian numbers are given explicitly by the sum
. The Eulerian numbers are given explicitly by the sum
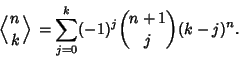 |
(1) |
| (2) | |||
| (3) |
| (4) |
| (5) |
The Eulerian numbers satisfy
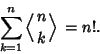 |
(6) |
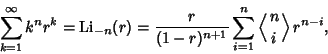 |
(7) |
See also Combination Lock, Euler Number, Euler's Triangle, Euler Zigzag Number, Polylogarithm, Sinc Function, Worpitzky's Identity, Z-Transform
References
Carlitz, L. ``Eulerian Numbers and Polynomials.'' Math. Mag. 32, 247-260, 1959.
Foata, D. and Schützenberger, M.-P. Théorie Géométrique des Polynômes Eulériens. Berlin: Springer-Verlag, 1970.
Kimber, A. C. ``Eulerian Numbers.'' Supplement to Encyclopedia of Statistical Sciences. (Eds. S. Kotz,
N. L. Johnson, and C. B. Read). New York: Wiley, pp. 59-60, 1989.
Salama, I. A. and Kupper, L. L. ``A Geometric Interpretation for the Eulerian Numbers.'' Amer. Math. Monthly
93, 51-52, 1986.
Sloane, N. J. A. Sequence
A008292
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
|
|
|
© 1996-9 Eric W. Weisstein