|
|
|
Let a combination of ![]() buttons be a Sequence of disjoint nonempty Subsets of the Set
buttons be a Sequence of disjoint nonempty Subsets of the Set
![]() . If the number of possible combinations is denoted
. If the number of possible combinations is denoted ![]() , then
, then ![]() satisfies the Recurrence
Relation
satisfies the Recurrence
Relation
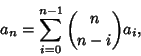 |
(1) |
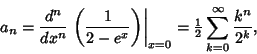 |
(2) |
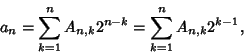 |
(3) |
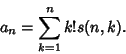 |
(4) |
| (5) |
The quantity
| (6) |
| (7) |
References
Sloane, N. J. A. Sequence
A000670/M2952
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Velleman, D. J. and Call, G. S. ``Permutations and Combination Locks.'' Math. Mag. 68, 243-253, 1995.