|
|
|
Given a Polynomial ![]() of degree
of degree ![]() with roots
with roots ![]() ,
, ![]() , ...,
, ..., ![]() and a Polynomial
and a Polynomial ![]() of degree
of degree ![]() with roots
with roots ![]() ,
, ![]() , ...,
, ..., ![]() , the resultant is defined by
, the resultant is defined by
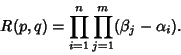
See also Discriminant (Polynomial), Sylvester Matrix
References
Pohst, M. and Zassenhaus, H. Algorithmic Algebraic Number Theory.
Cambridge, England: Cambridge University Press, 1989.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, p. 348, 1991.