|
|
|
An Integral Transform whose inverse is used to reconstruct images from medical CT scans. A technique for using Radon transforms to reconstruct a map of a planet's polar regions using a spacecraft in a polar orbit has also been devised (Roulston and Muhleman 1997).
The Radon transform can be defined by
|
|
|
|
|
(1) |
| (2) |
| (3) |
Using the identity
| (4) |
| (5) |
| (6) |
| (7) |
Nievergelt (1986) uses the inverse formula
| (8) |
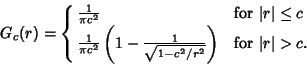 |
(9) |
| (10) | |||
| (11) |
The Radon transform satisfies superposition
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
The line integral along ![]() is
is
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
See also Tomography
References
Anger, B. and Portenier, C. Radon Integrals. Boston, MA: Birkhäuser, 1992.
Armitage, D. H. and Goldstein, M. ``Nonuniqueness for the Radon Transform.'' Proc. Amer. Math. Soc. 117, 175-178, 1993.
Deans, S. R. The Radon Transform and Some of Its Applications. New York: Wiley, 1983.
Durrani, T. S. and Bisset, D. ``The Radon Transform and its Properties.'' Geophys. 49, 1180-1187, 1984.
Esser, P. D. (Ed.). Emission Computed Tomography: Current Trends. New York: Society of Nuclear Medicine, 1983.
Gindikin, S. (Ed.). Applied Problems of Radon Transform. Providence, RI: Amer. Math. Soc., 1994.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, 1979.
Helgason, S. The Radon Transform. Boston, MA: Birkhäuser, 1980.
Kunyansky, L. A. ``Generalized and Attenuated Radon Transforms: Restorative Approach to the Numerical Inversion.''
Inverse Problems 8, 809-819, 1992.
Nievergelt, Y. ``Elementary Inversion of Radon's Transform.'' SIAM Rev. 28, 79-84, 1986.
Rann, A. G. and Katsevich, A. I. The Radon Transform and Local Tomography. Boca Raton, FL: CRC Press, 1996.
Robinson, E. A. ``Spectral Approach to Geophysical Inversion Problems by Lorentz, Fourier, and Radon
Transforms.'' Proc. Inst. Electr. Electron. Eng. 70, 1039-1053, 1982.
Roulston, M. S. and Muhleman, D. O. ``Synthesizing Radar Maps of Polar Regions with a Doppler-Only Method.'' Appl. Opt.
36, 3912-3919, 1997.
Shepp, L. A. and Kruskal, J. B. ``Computerized Tomography: The New Medical X-Ray Technology.'' Amer. Math. Monthly 85,
420-439, 1978.
Strichartz, R. S. ``Radon Inversion--Variation on a Theme.'' Amer. Math. Monthly 89, 377-384 and 420-423, 1982.
Zalcman, L. ``Uniqueness and Nonuniqueness for the Radon Transform.'' Bull. London Math. Soc. 14, 241-245, 1982.
![]() Radon Transforms
Radon Transforms
|
|
|
© 1996-9 Eric W. Weisstein