|
|
|
Let ![]() be a continuous function and
be a continuous function and ![]() and
and ![]() be Fourier Transform pairs so that
be Fourier Transform pairs so that
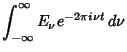 |
(1) | ||
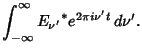 |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
For finite Fourier Transform pairs ![]() and
and ![]() ,
,
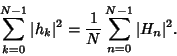 |
(4) |
If a function has a Fourier Series given by
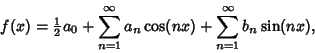 |
(5) |
|
|
|
|
|
|
|
|
|
|
|
(6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
![\begin{displaymath}
{1\over\pi}\int^{\pi}_{-\pi} [f(x)]^2\,dx ={\textstyle{1\over 2}}{a_0}^2 + \sum_{n=1}^\infty ({a_n}^2+{b_n}^2).
\end{displaymath}](p1_663.gif) |
(8) |
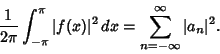 |
(9) |
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1101, 1979.