|
|
|
A Gaussian Quadrature-like formula for numerical estimation of integrals. It requires ![]() points and fits all
Polynomials to degree
points and fits all
Polynomials to degree ![]() , so it effectively fits exactly all Polynomials of
degree
, so it effectively fits exactly all Polynomials of
degree ![]() . It uses a Weighting Function
. It uses a Weighting Function ![]() in which the endpoint
in which the endpoint ![]() in the interval
in the interval ![]() is included
in a total of
is included
in a total of ![]() Abscissas, giving
Abscissas, giving ![]() free abscissas. The general formula is
free abscissas. The general formula is
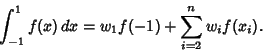 |
(1) |
| (2) |
| (3) |
| (4) |
| (5) |
| 2 | 0.5 | |
| 0.333333 | 1.5 | |
| 3 | 0.222222 | |
| 1.02497 | ||
| 0.689898 | 0.752806 | |
| 4 | 0.125 | |
| 0.657689 | ||
| 0.181066 | 0.776387 | |
| 0.822824 | 0.440924 | |
| 5 | 0.08 | |
| 0.446208 | ||
| 0.623653 | ||
| 0.446314 | 0.562712 | |
| 0.885792 | 0.287427 |
The Abscissas and weights can be computed analytically for small ![]() .
.
| 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
See also Chebyshev Quadrature, Lobatto Quadrature
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 888, 1972.
Chandrasekhar, S. Radiative Transfer. New York: Dover, p. 61, 1960.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 338-343,
1956.
|
|
|
© 1996-9 Eric W. Weisstein