|
|
|
Also called Radau Quadrature (Chandrasekhar 1960). A Gaussian Quadrature with Weighting Function ![]() in which the endpoints of the interval
in which the endpoints of the interval ![]() are included in a total of
are included in a total of ![]() Abscissas, giving
Abscissas, giving ![]() free
abscissas. Abscissas are symmetrical about the origin, and the general Formula is
free
abscissas. Abscissas are symmetrical about the origin, and the general Formula is
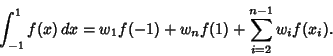 |
(1) |
| (2) | |||
| (3) |
| (4) |
| (5) |
| 3 | 0 | 1.33333 |
| ± 1 | 0.333333 | |
| 4 | ± 0.447214 | 0.833333 |
| ± 1 | 0.166667 | |
| 5 | 0 | 0.711111 |
| ± 0.654654 | 0.544444 | |
| ± 1 | 0.100000 | |
| 6 | ± 0.285232 | 0.554858 |
| ± 0.765055 | 0.378475 | |
| ± 1 | 0.0666667 |
The Abscissas and weights can be computed analytically for small ![]() .
.
| 3 | 0 |
|
|
|
||
| 4 |
|
|
|
|
||
| 5 | 0 |
|
|
|
|
|
|
|
See also Chebyshev Quadrature, Radau Quadrature
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 888-890, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 465, 1987.
Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 63-64, 1960.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 343-345, 1956.
|
|
|
© 1996-9 Eric W. Weisstein