|
|
|
The probability density function ![]() (also called the Probability Density Function) of a continuous distribution is
defined as the derivative of the (cumulative) Distribution Function
(also called the Probability Density Function) of a continuous distribution is
defined as the derivative of the (cumulative) Distribution Function ![]() ,
,
| (1) |
| (2) |
A probability density function satisfies
| (3) |
| (4) |
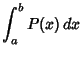 |
(5) | ||
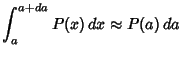 |
(6) | ||
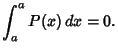 |
(7) |
If ![]() and
and ![]() , then
, then
| (8) |
Given the Moments of a distribution (![]() ,
, ![]() , and the Gamma Statistics
, and the Gamma Statistics
![]() ), the asymptotic probability function is given by
), the asymptotic probability function is given by
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9) |
| (10) |
| (11) |
See also Continuous Distribution, Cornish-Fisher Asymptotic Expansion, Discrete Distribution, Distribution Function, Joint Distribution Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Probability Functions.'' Ch. 26 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 925-964, 1972.
|
|
|
© 1996-9 Eric W. Weisstein