|
|
|
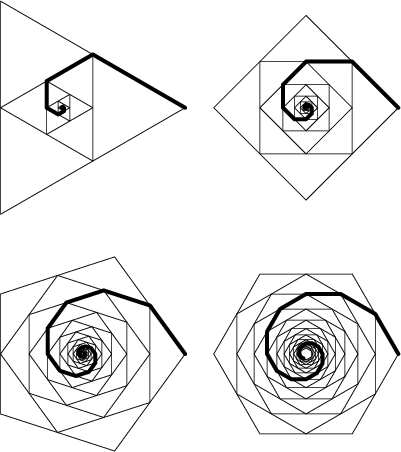
The length of the polygonal spiral is found by noting that the ratio of Inradius to Circumradius
of a regular Polygon of ![]() sides is
sides is
| (1) |
![\begin{displaymath}
L={\textstyle{1\over 2}}s\sum_{k=0}^\infty \cos^k\left({\pi\...
...ght)={s\over 2\left[{1-\cos\left({\pi\over n}\right)}\right]}.
\end{displaymath}](p2_1389.gif) |
(2) |
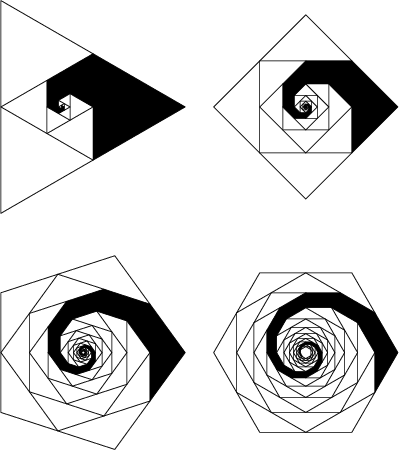
Consider the solid region obtained by filling in subsequent triangles which the spiral encloses. The Area of
this region, illustrated above for ![]() -gons of side length
-gons of side length ![]() , is
, is
| (3) |
References
Sandefur, J. T. ``Using Self-Similarity to Find Length, Area, and Dimension.'' Amer. Math. Monthly 103, 107-120, 1996.