Given a Parabola
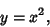 |
(1) |
the parametric equation and its derivatives are
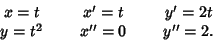 |
(2) |
The Radius of Curvature is
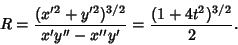 |
(3) |
The Tangent Vector is
![\begin{displaymath}
\hat {\bf T} = {1\over\sqrt{1+4t^2}} \left[{\matrix{1\cr 2t\cr}}\right],
\end{displaymath}](p1_310.gif) |
(4) |
so the parametric equations of the evolute are
and
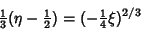 |
(9) |
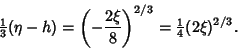 |
(10) |
The Evolute is therefore
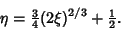 |
(11) |
This is known as Neile's Parabola and is a Semicubical Parabola. From a point above the evolute three
normals can be drawn to the Parabola, while only one normal can be drawn to the Parabola from a point
below the Evolute.
See also Neile's Parabola, Parabola, Semicubical Parabola
© 1996-9 Eric W. Weisstein
1999-05-26