A 4-D space with the Minkowski Metric. Alternatively, it can be considered to have a Euclidean Metric, but
with its Vectors defined by
![\begin{displaymath}
\left[{\matrix{x_0\cr x_1\cr x_2\cr x_3\cr}}\right] = \left[{\matrix{ict\cr x\cr y\cr z\cr}}\right],
\end{displaymath}](m_1282.gif) |
(1) |
where 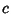 is the speed of light.
is the speed of light.  The Metric is Diagonal with
The Metric is Diagonal with
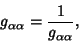 |
(2) |
so
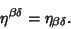 |
(3) |
Let 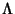 be the Tensor for a Lorentz Transformation. Then
be the Tensor for a Lorentz Transformation. Then
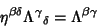 |
(4) |
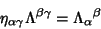 |
(5) |
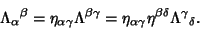 |
(6) |
The Necessary and Sufficient conditions for a metric 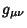 to be equivalent to the Minkowski metric
to be equivalent to the Minkowski metric
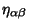 are that the Riemann Tensor vanishes everywhere (
are that the Riemann Tensor vanishes everywhere (
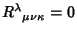 ) and that at
some point
) and that at
some point 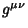 has three Positive and one Negative Eigenvalues.
has three Positive and one Negative Eigenvalues.
See also Lorentz Transformation, Minkowski Metric
References
Thompson, A. C. Minkowski Geometry. New York: Cambridge University Press, 1996.
© 1996-9 Eric W. Weisstein
1999-05-26
![\begin{displaymath}
\left[{\matrix{x_0\cr x_1\cr x_2\cr x_3\cr}}\right] = \left[{\matrix{ict\cr x\cr y\cr z\cr}}\right],
\end{displaymath}](m_1282.gif)