A 4-D transformation satisfied by all Four-Vectors 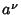 ,
,
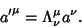 |
(1) |
In the theory of special relativity,  the Lorentz transformation replaces the
Galilean Transformation as the valid transformation law between reference frames moving with respect to one another
at constant Velocity. Let
the Lorentz transformation replaces the
Galilean Transformation as the valid transformation law between reference frames moving with respect to one another
at constant Velocity. Let 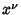 be the Position Four-Vector with
be the Position Four-Vector with 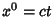 , and let the relative motion be
along the
, and let the relative motion be
along the 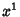 axis with Velocity
axis with Velocity 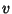 . Then (1) becomes
. Then (1) becomes
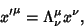 |
(2) |
where the Lorentz Tensor is given by
![\begin{displaymath}
{\hbox{\sf L}} =\left[{\matrix{
\Lambda_0^0 & \Lambda_1^0 & ...
... \gamma & 0 & 0\cr
0 & 0 & 1 & 0\cr
0 & 0 & 0 & 1\cr}}\right].
\end{displaymath}](l2_923.gif) |
(3) |
Here,
Written explicitly, the transformation between 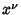 and
and 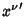 coordinate is
coordinate is
The Determinant of the upper left 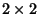 Matrix in (3) is
Matrix in (3) is
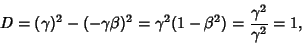 |
(10) |
so
A Lorentz transformation along the 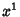 -axis can also be written
-axis can also be written
![\begin{displaymath}
\left[{\matrix{{x^0}'\cr {x^1}'\cr {x^2}'\cr {x^3}'\cr}}\rig...
...] \left[{\matrix{{x^0}\cr {x^1}\cr {x^2}\cr {x^3}\cr}}\right],
\end{displaymath}](l2_937.gif) |
(11) |
where 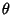 is called the rapidity,
is called the rapidity, 
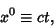 |
(12) |
and
See also Hyperbolic Rotation, Lorentz Group, Lorentz Tensor
References
Fraundorf, P. ``Accel-1D: Frame-Dependent Relativity at UM-StL.''
http://www.umsl.edu/~fraundor/a1toc.html.
Griffiths, D. J. Introduction to Electrodynamics. Englewood Cliffs, NJ: Prentice-Hall, pp. 412-414, 1981.
Morse, P. M. and Feshbach, H. ``The Lorentz Transformation, Four-Vectors, Spinors.'' §1.7 in
Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 93-107, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
,
![\begin{displaymath}
{\hbox{\sf L}} =\left[{\matrix{
\Lambda_0^0 & \Lambda_1^0 & ...
... \gamma & 0 & 0\cr
0 & 0 & 1 & 0\cr
0 & 0 & 0 & 1\cr}}\right].
\end{displaymath}](l2_923.gif)
![$\displaystyle \left[\begin{array}{ccccccccccccc}
(\Lambda^{-1})_0^0 & (\Lambda^...
...^{-1})_1^3 & (\Lambda^{-1})_2^3 & (\Lambda^{-1})_3^3\end{array}\right]\nonumber$](l2_935.gif)
![$\displaystyle \left[\begin{array}{ccccccccccccc}
\gamma & \gamma\beta & 0 & 0\\...
... & 0 & 0\nonumber\\
0 & 0 & 1 & 0\nonumber\\
0 & 0 & 0 & 1\end{array}\right].$](l2_936.gif)
![]() -axis can also be written
-axis can also be written
![\begin{displaymath}
\left[{\matrix{{x^0}'\cr {x^1}'\cr {x^2}'\cr {x^3}'\cr}}\rig...
...] \left[{\matrix{{x^0}\cr {x^1}\cr {x^2}\cr {x^3}\cr}}\right],
\end{displaymath}](l2_937.gif)