Four-Vector

A four-element vector

$$a^\mu =\left[{\matrix{a^0\cr a^1\cr a^2\cr a^3\cr}}\right],$$ (1)

which transforms under a Lorentz Transformation like the Position Four-Vector. This means it obeys

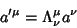$$a'^\mu = \Lambda_\nu^\mu a^\nu$$ (2)

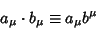$$a_\mu\cdot b_\mu\equiv a_\mu b^\mu$$ (3)

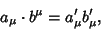$$a_\mu\cdot b^\mu = a_\mu'b_\mu',$$ (4)

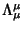where $\Lambda_\mu^\mu$ is the Lorentz Tensor. Multiplication of two four-vectors with the Metric 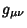$g_{\mu\nu}$ gives products of the form

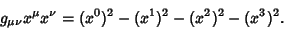$$g_{\mu\nu}x^\mu x^\nu=(x^0)^2-(x^1)^2-(x^2)^2-(x^3)^2.$$ (5)

In the case of the Position Four-Vector, 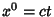$x^0=ct$ (where 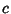$c$ is the speed of light ) and this product is an invariant known as the spacetime interval.

See also Gradient Four-Vector, Lorentz Transformation, Position Four-Vector, Quaternion

References

Morse, P. M. and Feshbach, H. ``The Lorentz Transformation, Four-Vectors, Spinors.'' §1.7 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 93-107, 1953.