|
|
|
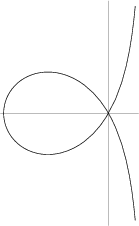
A curve first studied by Colin Maclaurin ![]() in 1742. It was studied to provide a solution to one of the
Geometric Problems of Antiquity, in particular Trisection of an Angle, whence the name trisectrix.
The Maclaurin trisectrix is an Anallagmatic Curve, and the origin is a Crunode.
in 1742. It was studied to provide a solution to one of the
Geometric Problems of Antiquity, in particular Trisection of an Angle, whence the name trisectrix.
The Maclaurin trisectrix is an Anallagmatic Curve, and the origin is a Crunode.
The Maclaurin trisectrix has Cartesian equation
| (1) |
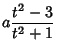 |
(2) | ||
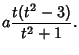 |
(3) |
The Maclaurin trisectrix is sometimes defined instead as
| (4) |
| (5) |
| (6) |
| (7) |
The tangents to the curve at the origin make angles of ![]() with the x-Axis. The Area of the
loop is
with the x-Axis. The Area of the
loop is
| (8) |
The Maclaurin trisectrix is the Pedal Curve of the Parabola where the Pedal Point is taken as the reflection of the Focus in the Directrix.
See also Right Strophoid, Tschirnhausen Cubic
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 103-106, 1972.
Lee, X. ``Trisectrix.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Trisectrix_dir/trisectrix.html.
Lee, X. ``Trisectrix of Maclaurin.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/TriOfMaclaurin_dir/triOfMaclaurin.html
MacTutor History of Mathematics Archive. ``Trisectrix of Maclaurin.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Trisectrix.html.
|
|
|
© 1996-9 Eric W. Weisstein