|
|
|
The Strophoid of a line ![]() with pole
with pole ![]() not on
not on ![]() and fixed point
and fixed point ![]() being the point where the
Perpendicular from
being the point where the
Perpendicular from ![]() to
to ![]() cuts
cuts ![]() is called a right strophoid. It is therefore a general Strophoid with
is called a right strophoid. It is therefore a general Strophoid with
![]() .
.
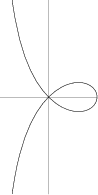
The right strophoid is given by the Cartesian equation
| (1) |
| (2) |
| (3) | |||
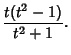 |
(4) |
| (5) |
| (6) |
The right strophoid first appears in work by Isaac Barrow in 1670, although Torricelli describes the curve in his letters
around 1645 and Roberval found it as the Locus of the focus of the conic obtained when the plane cutting the
Cone rotates about the tangent at its vertex (MacTutor Archive). The Area of the loop is
| (7) |
Let ![]() be the Circle with center at the point where the right strophoid crosses
the
be the Circle with center at the point where the right strophoid crosses
the ![]() -axis and radius the distance of that point from the origin. Then the right
strophoid is invariant under inversion in the Circle
-axis and radius the distance of that point from the origin. Then the right
strophoid is invariant under inversion in the Circle ![]() and is
therefore an Anallagmatic Curve.
and is
therefore an Anallagmatic Curve.
See also Strophoid, Trisectrix
References
Gray, A. Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, p. 71, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 100-104, 1972.
Lockwood, E. H. ``The Right Strophoid.'' Ch. 10 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 90-97, 1967.
MacTutor History of Mathematics Archive. ``Right Strophoid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Right.html.
|
|
|
© 1996-9 Eric W. Weisstein